
One of Latin America’s largest providers of hydroelectric energy in Colombia and Latin America has invested heavily in becoming a hydroelectric backbone in the last five years. Before undertaking a hydroelectric project, the utility company considers the cost implications of constructing a plant. To determine the project viability and profitability of constructing a new plant, it is important to accurately estimate the quantities and the unit cost of items needed for construction. To do this, the company turned to Palisade’s @RISK software to accurately estimate the budget via a stochastic model based on uncertainty and risk profiles for quantities and prices of key construction elements.
The Need for Traditional Versus Stochastic Analysis
The utility’s power plants often need to be built underground. Due to the high risks and uncertainty involved in subterranean construction, it is important to accurately assess the budget implications during the planning stage to define the project's viability.
Many organizations add an additional percentage to costs in order to account for uncertainty and risk conditions in preparing a budget. However, this is an inadequate process of estimation as these additional costs may not be appropriate for the project. An inadequate estimate can lead to projects going over budget, or projects not being undertaken due to excessive cost forecasts.
A better solution for estimating the budget is stochastic modeling to account for uncertainty, using risk profiles for quantities and prices. Stochastic modeling means simply including ranges of values for uncertain factors in the analysis. From this, an accurate probability distribution can be calculated for a budget.
@RISK at Work
Before embarking on the construction of a hydroelectric power project, the company estimates the funding required using financial indicators such as Net Present Value (NPV) and Internal rate of Return (IRR). In addition, it also needs to optimize the procurement scheme, estimate the Probable Maximum Loss (PML) to insure the project, define insurance policies and thereby assess the cost of risk. The cost assessment can be hampered by uncertainty and risk conditions, which are implicit in the quantities and unit cost of each item of in the budget. Using @RISK, these uncertainties are accounted for in order to develop a probabilistic picture of the budget needed for each project.
Three Different Budgets
Using @RISK, the company calculates three different budget “views” of a project:
-A deterministic one that does not consider the variation and risk in prices and quantities of key project components. As a result, it resembles a snapshot of the project because it is (unrealistically) static. -A Stochastic one that only considers the expected variations that the project can have in quantities and prices. -Finally, a stochastic model with risk that considered the expected variations and the unexpected events (risk) that the project can have in quantities and prices.
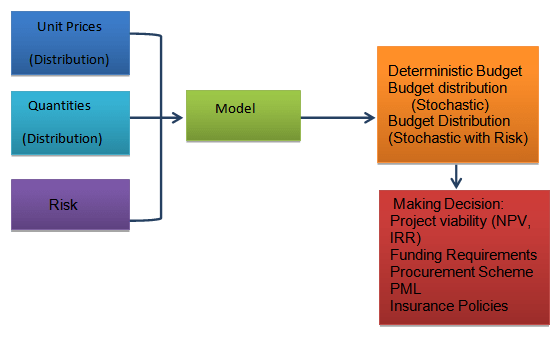
The differences between these three calculations are considered in order to understand the importance of considering variation and unexpected events in a project and to analyze the different impacts.
Head of Risk and Insurance Strategy at hydroelectric power plant
A Sample Project
In one recent project, the utility company used the following probability distribution functions in @RISK to describe uncertainty inherent in the prices and quantities of project components:
Discrete Distribution
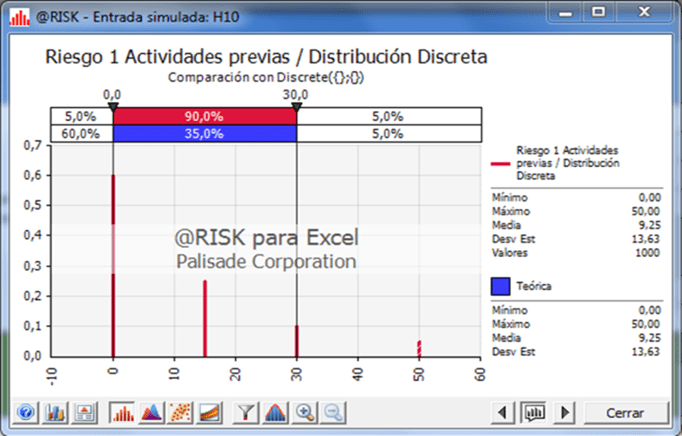
Discrete distribution: The Discrete distribution was utilized for any unexpected events where they were able find more than three values utilizing expert advice and judgment. A Triangle Distribution
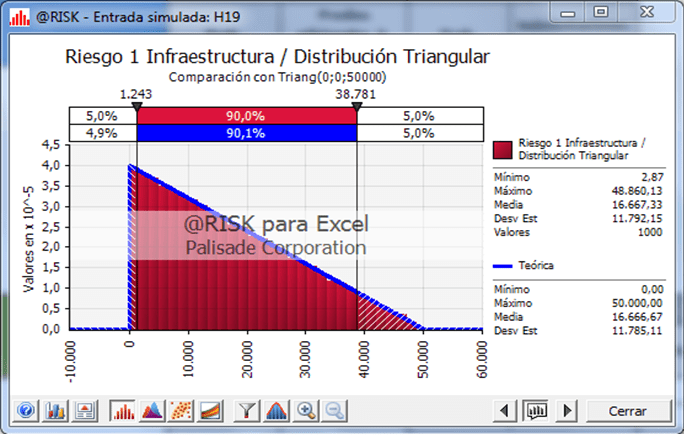
Triangular distribution: Due to the limited amount of market data, the company utilized expert advice and judgment to construct this simple but accurate distribution. The Triangular distribution requires only pieces of information: minimum, most likely, and maximum. A Bernoulli Distribution
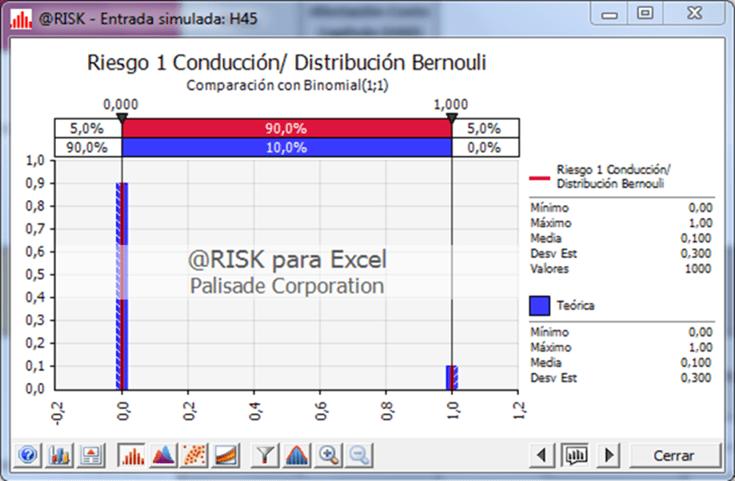
Bernoulli: The Bernoulli distribution was utilized for unexpected events which occur infrequently. The distribution considers the probability of occurrence and non-occurrence of events. The model tracked the simulation of several different outputs, such as the cost associated with different work streams and the calculation of the total budget of the project.
Simulation Results
Significant differences in the distribution profiles between the three budgetary views were discovered. In the deterministic model, no consideration was given to how likely input variables were to change. Instead, simple point estimates were used to “guess” best case, worse case, and most likely scenarios.
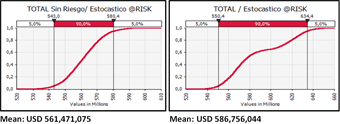
In the stochastic @RISK model where inputs were allowed to vary according expectations, the company found that expected total project cost was higher than the deterministic model forecast, and was able to see over what range the total project cost could vary. The mean was around $560 million, but, just as importantly, the total project risked creeping up to around $595 million. In fact, there was a 50% of exceeding the expected cost.
When the stochastic @RISK model was allowed to consider unexpected events, the mean total cost creeped higher – to around $586 million. In addition, two broad scenarios became apparent – one where risk events didn’t occur and let to a cost of around $570 million, and another scenario where more did occur with a total cost of $620 million! These insights helped the utility company make better plans for contingencies, procurement, design control, vendor terms, and financing. It helped identify key risks driving these results, and their economic implications on budgets for individual work and the total project. Overall, it helped determine the technical and economic feasibility of the project.
Stochastic Stochastic Considering Risk
“The most accurate budget calculation for the project is the model which considers the variability and risk in quantities and prices,” said the company’s head of risk and insurance strategy. “Using @RISK, we were able to use the Monte Carlo simulation to create many different scenarios to approximate reality. Software features such as fit distribution, adding distributions to a cell and simulation data are extremely helpful when evaluating various possibilities.”
