Request demo
Buy now
0
$0.00 0 items

No products in the cart.

Mitigate Risks

Monte Carlo Simulation in Excel

Calculate many different outcomes and their probabilities of occurring with Monte Carlo simulation software.

Monte Carlo Analysis Probabilistically Assesses the Impact of Risk

As we are constantly faced with uncertainty and variability, risk and forecast analysis is part of every decision you make. And even though we have unprecedented access to information, we can’t accurately forecast the future. But with Monte Carlo simulation, we have the next best thing to a superpower.

The Monte Carlo method lets you see all possible outcomes of your decisions, including the actual probabilities each will occur, by running simulations with random variables thousands of times. These random numbers are described by their probability distribution which can be estimated with historical data or defined using expert opinion. Then, with risk analysis software like @RISK, you can run sensitivity analysis to identify which variables have the largest impact on the outcome. This method lets you quantitatively assess the impact of risk, allowing for more accurate forecasting and, ultimately, better decision-making under uncertainty.

What is Monte Carlo Simulation?

The Monte Carlo simulation is a mathematical technique that models the probability of different events occurring -- allowing people to quantitatively account for risk in forecasting and decision-making. At its core, the Monte Carlo method is a way to use repeating random samples of parameters to explore the behavior of a complex system. A Monte Carlo analysis is used to estimate and handle an extensive range of problems in a variety of different fields to understand the impact of risk and uncertainty

A Way to Account for and Simulate Risk

Monte Carlo simulations have assessed the impact of risk in cost estimation, project management, portfolio optimization, and many other real-life scenarios. The Monte Carlo method provides many advantages over predictive models with fixed inputs, such as the ability to conduct sensitivity analysis or define correlation between inputs.

A Forecast Analysis Tool That Works in Many Fields

The technique is used for forecasting which takes into account risk and can simulate demand forecasting, load planning, pricing, sales forecasting, portfolio allocation, strategic planning, Six Sigma and quality control, profit projects, and more. Using this method, one can easily take risks into account and compute the probability of completing a project on time and staying within budget.

Use cases run the gamut and include cash flow analysis, capital investments, reserves estimation, pricing, cost estimation, project management, product pipeline analysis, portfolio optimization, supply chain risk, and more.
Monte Carlo analysis is used in many different fields, including:
Environmental Conservation
Agriculture & Food Safety
Consulting & Legal
Entertainment, Sports & Media
Mining & Minerals
Technology & Telecom

A Range of Outcomes Using Random Variables

A Monte Carlo experiment furnishes the decision-maker with a range of possible outcomes and the probabilities they will occur for any choice of action. It shows:
The outcomes of going for broke and for the most conservative decision
Along with all possible consequences for middle-of-the-road decisions

History of Monte Carlo Method

The technique was invented by John von Neumann and Stanislaw Ulam and first used by scientists working on the atom bomb; it was named for Monte Carlo, the Monaco resort town renowned for its casinos. Since its introduction in World War II, Monte Carlo simulation has been used to model a variety of physical and conceptual systems.

How Monte Carlo Analysis in Microsoft Excel Works

A Monte Carlo experiment performs risk analysis by building models of possible results by substituting a range of values—called a probability distribution—for any factor that has inherent uncertainty. It then calculates results over and over, each time using a different set of random values from the input probability distributions. Depending upon the number of uncertainties and the ranges specified for them, a Monte Carlo analysis could involve thousands or tens of thousands of recalculations before it is complete. The result of the experiment is a range – or distribution – of possible outcome values. This data on possible results enables you to calculate the probabilities of different outcomes in your forecasts, as well as perform a wide range of additional analyses. Monte Carlo simulation software builds a spreadsheet model that lets you evaluate your plan numerically, allowing you to change the numbers, ask ‘what if’ and see the results.
By using probability distributions for uncertain inputs, you can represent the different possible values for these uncertain variables, along with their likelihood of occurrence. Probability distributions are a much more realistic way of describing uncertainty in variables of a risk analysis, making Monte Carlo simulation far superior to common “best guess” or “best/worst/most likely” analyses.

To use the Monte Carlo method, you need to build a qualitative model of your business activity, plan, or process. The best way to do this is by creating a spreadsheet model using Microsoft Excel and using Lumivero's @RISK analysis software. Analyze your simulation results by using the mean, percentiles, standard deviation, in addition to charts and graphs. Lumivero's @RISK software will help you interpret your data and is backed by 24/7 technical support and assistance.

100% Microsoft Excel Integration

With PrecisionTree, you never leave your spreadsheet, allowing you to work in a familiar environment, and get up to speed quickly.

Full Statistics Reports and Graphs

See results in risk profile graphs, 2-way sensitivity, tornado graphs, spider graphs, policy suggestion reports, and strategy-region graphs.

Bayesian Revision

“Flip” one or more chance nodes to show probabilities calculated using Bayes’ Rule. This is valuable when the probabilities of a model are not available in a directly useful form. For example: You need to know the probability of an outcome occurring given the results of a particular test. The test’s accuracy may be known, but the only way to determine the probability you seek is to “reverse” a traditional decision tree in Microsoft Excel using Bayes Rule.

Advanced Features

Set up your decision tree in Microsoft Excel exactly as you need it with logic nodes, reference nodes, linked trees, custom utility functions, and influence diagrams.

Common Probability Distributions and Models

FEATURES LIST (not always shown)

FeatureBenefitProfessional EditionIndustrial Edition
Optimization under uncertaintyCombines Monte Carlo simulation with sophisticated optimization techniques to find optimal solutions to uncertain problems. Used for budgeting, allocation, scheduling, and more.
Efficient Frontier AnalysisEspecially useful in financial analysis, Efficient Frontiers determine the optimal return that can be expected from a portfolio at a given level of risk
Ranges for adjustable cells and constraintsStreamlined model setup and editing
Genetic algorithmsFind the best global solution while avoiding getting caught in local, “hill-climbing” solutions
Six solving methods, including GAs and OptQuestAlways have the best method for different types of problems
RISKOptimizer Watcher and Convergence MonitoringMonitor progress toward best solutions in real time
Overlay of Optimized vs Original DistributionCompare original output to optimized result to visually see improvements
Original, Best, Last model updatingInstantly see the effects of three solutions on your entire model

Random Sampling Versus Best Guess

During a Monte Carlo experiment, values are sampled at random from the input probability distributions. Each set of samples is called an iteration, and the resulting outcome from that sample is recorded. Monte Carlo simulation does this process hundreds or thousands of times, and the result is a probability distribution of possible outcomes. In this way, Monte Carlo simulation provides a much more comprehensive view of what may happen. It tells you not only what could happen, but how likely it is to happen.

Monte Carlo simulation provides several advantages over deterministic, or “single-point estimate” analysis:
Probabilistic Results. Results show not only what could happen, but how likely each outcome is.
Graphical Results. Because of the data a Monte Carlo experiment generates, it’s easy to create graphs of different outcomes and their chances of occurrence. This is important for communicating findings to other stakeholders.
Sensitivity Analysis. Deterministic analysis makes it difficult to see which variables impact the outcome the most. In Monte Carlo simulation, it’s easy to see which inputs had the biggest effect on bottom-line results. This allows you to identify and mitigate factors which cause the most risk.
Scenario Analysis: Scenario analysis determines which input variables contribute significantly toward reaching a particular goal (called the target scenario or output scenario) associated with an output. For example, it can show which variables contribute to exceptionally high sales values or which variables contribute to negative NPV values.
Correlation of Inputs. In Monte Carlo analysis, it’s possible to model interdependent relationships between input variables. It’s important for accuracy to represent how, in reality, when some factors go up or down, others go up or down accordingly.
An enhancement to Monte Carlo experiment is the use of Latin Hypercube sampling which samples more accurately from the full range of values within distribution functions and produces results more quickly.

Resources

Predictive Neural Networks

Sophisticated, predictive neural networks imitate brain functions to identify patterns in historical or new, incomplete data sets – letting you intelligently predict the future and...

Read more

Enterprise Licensing
Better Research, Insights, and Outcomes for All

Whether your organization’s focus is qualitative, quantitative, or mixed methods data analysis, we can help your whole team work better together — collaborating to aggregate, organize, analyze, and present your findings. Lumivero’s enterprise licensing options offer volume pricing for teams and organizations needing nine (9) or more licenses.

Enterprise licenses allow the flexibility to install Lumivero software and solutions on multiple computers (up to the maximum number of licenses that your site has purchased) with a centralized management solution.

Lumivero’s team-based solutions allow you to:

Stay up-to-date with free upgrades to the latest releases
Reduce IT costs with one platform deployed across your organization
Reassign licenses to different users as teams evolve
Centralize license and subscription management in one place
Streamline budget allocation, especially for smaller groups and consultancy firms
Enjoy a Dedicated Customer Success Manager and pro-rated rates for new users

Use Monte Carlo Simulation
with Lumivero's @RISK and DecisionTools Suite

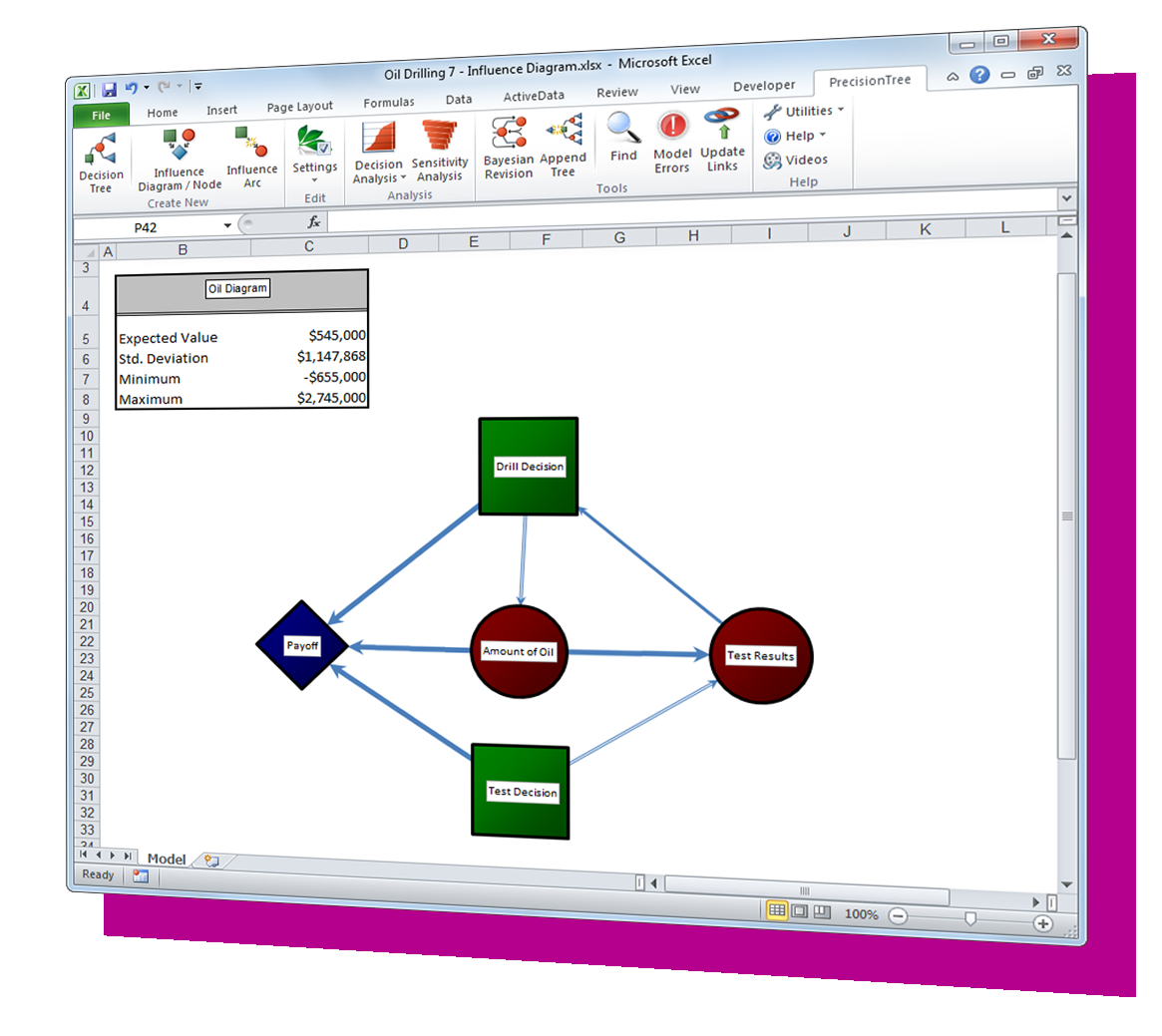
Lumivero’s @RISK software puts this powerful technique within reach for any Excel user faced with uncertainty in their analyses. @RISK makes it easy to graphically define risk models, run simulations, and analyze the results, all with the click of a mouse. @RISK is 100% integrated with Excel, adding hundreds of new functions to Excel so that users can quickly understand their risks without learning a new application. First introduced in 1987 for Lotus 1-2-3, @RISK has a long-established reputation for computational accuracy, modeling flexibility, and ease of use, making it the dominant Monte Carlo simulation software in the market today.

More About @RISK
magnifierarrow-right
linkedin facebook pinterest youtube rss twitter instagram facebook-blank rss-blank linkedin-blank pinterest youtube twitter instagram