| Feature | Benefit | Professional Edition | Industrial Edition |
|---|---|---|---|
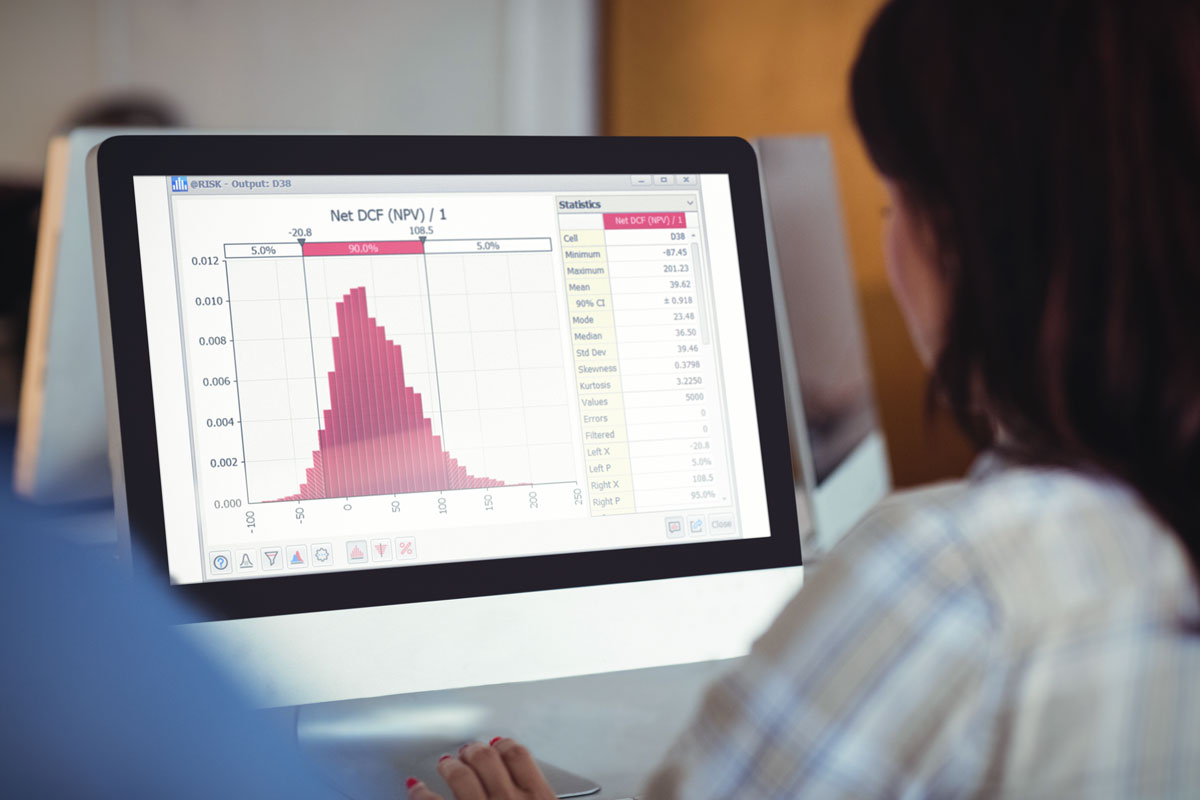
| Optimization under uncertainty | Combines Monte Carlo simulation with sophisticated optimization techniques to find optimal solutions to uncertain problems. Used for budgeting, allocation, scheduling, and more. |  |  |
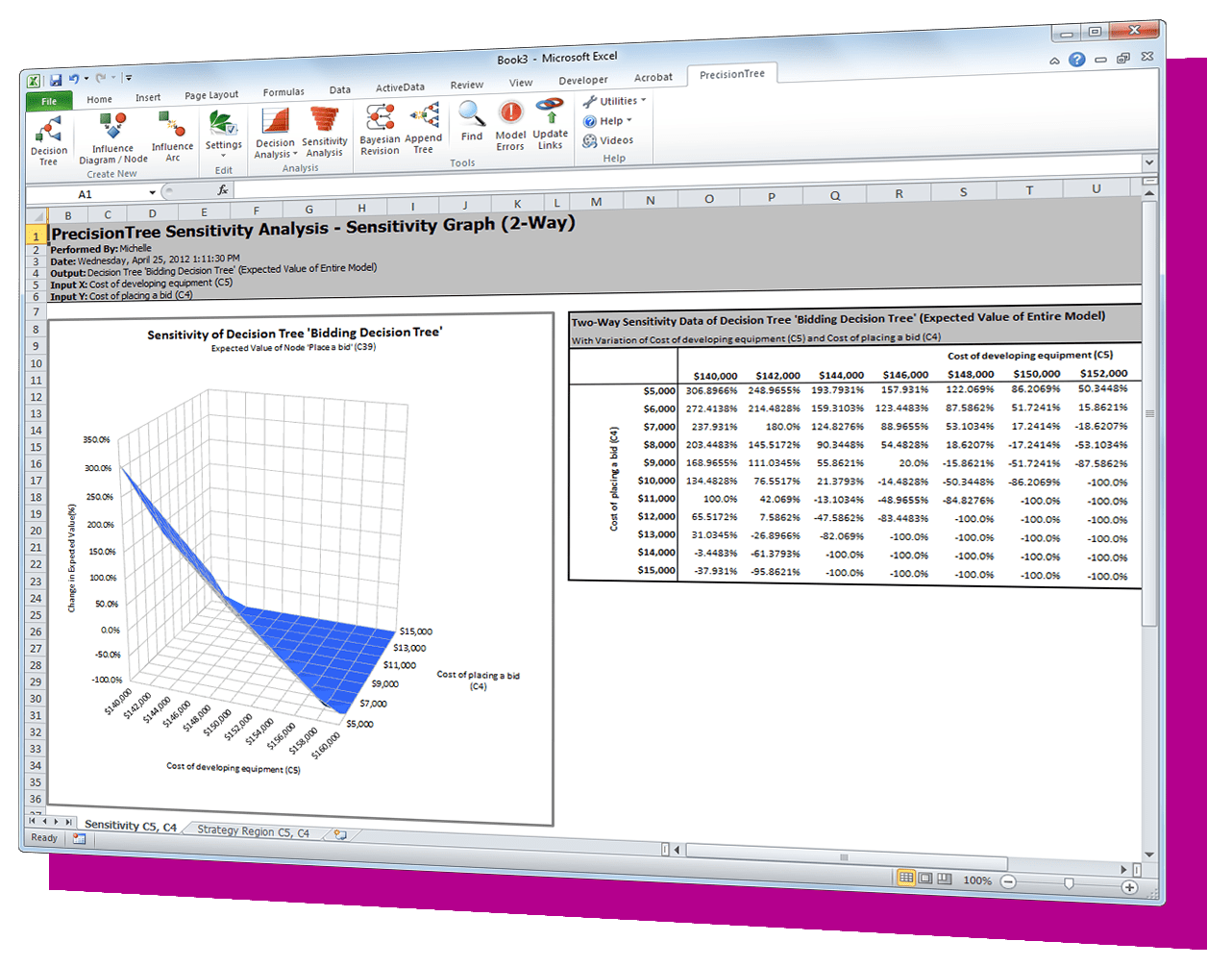
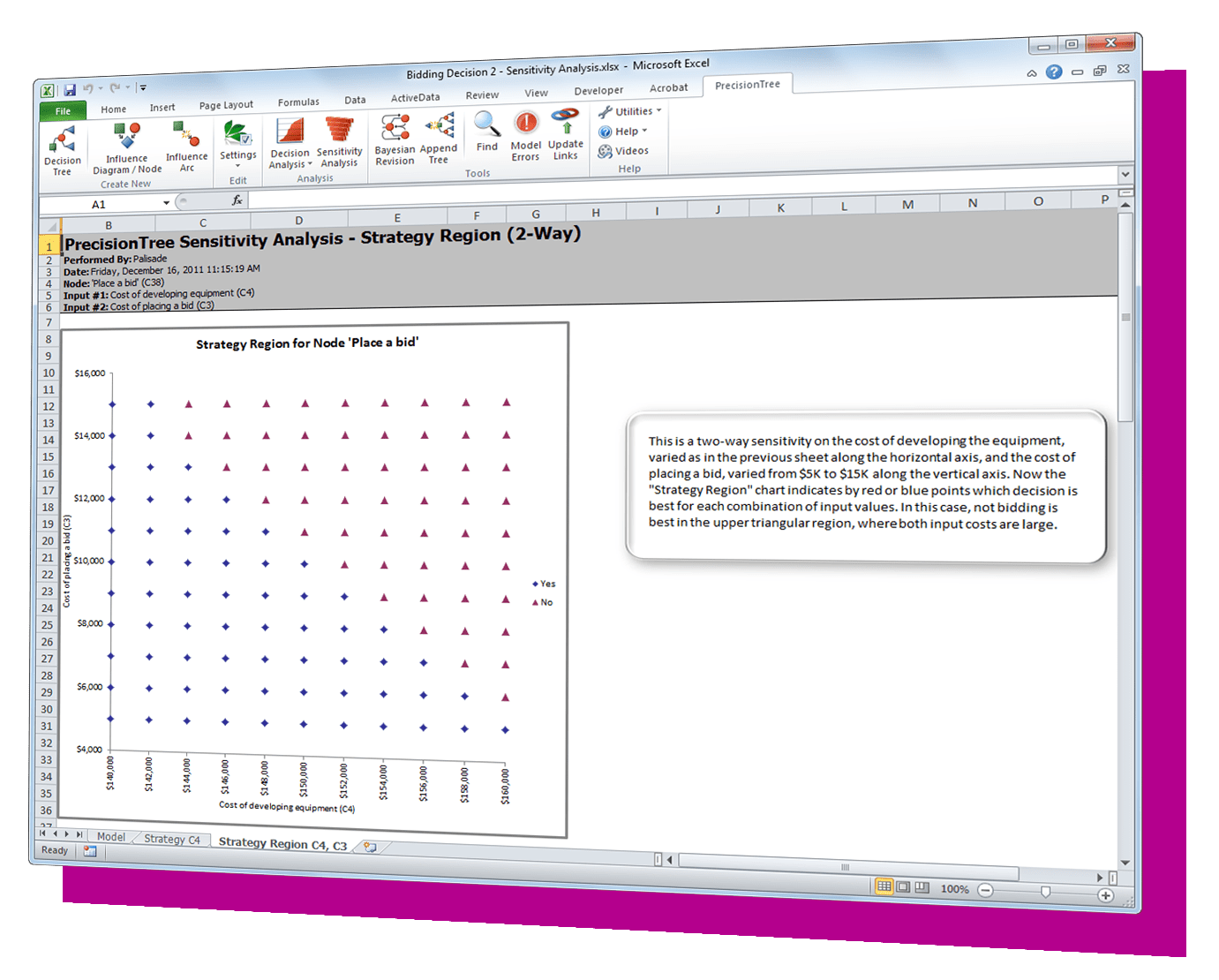
| Efficient Frontier Analysis | Especially useful in financial analysis, Efficient Frontiers determine the optimal return that can be expected from a portfolio at a given level of risk |  |  |
| Ranges for adjustable cells and constraints | Streamlined model setup and editing |  |  |
| Genetic algorithms | Find the best global solution while avoiding getting caught in local, “hill-climbing” solutions |  |  |
| Six solving methods, including GAs and OptQuest | Always have the best method for different types of problems |  |  |
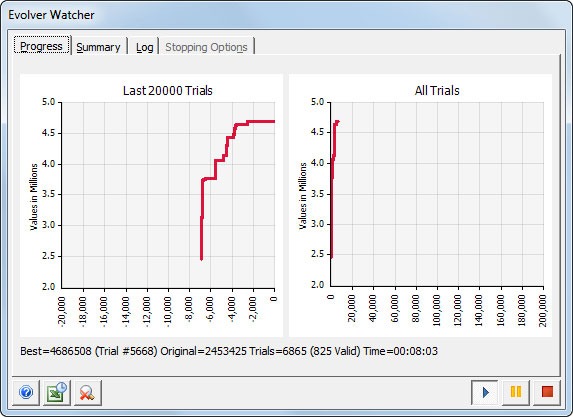
| RISKOptimizer Watcher and Convergence Monitoring | Monitor progress toward best solutions in real time |  |  |
| Overlay of Optimized vs Original Distribution | Compare original output to optimized result to visually see improvements |  |  |
| Original, Best, Last model updating | Instantly see the effects of three solutions on your entire model |  |  |
| Feature | Benefit | Professional Edition | Industrial Edition |
|---|---|---|---|
| Optimization under uncertainty | Combines Monte Carlo simulation with sophisticated optimization techniques to find optimal solutions to uncertain problems. Used for budgeting, allocation, scheduling, and more. |  |  |
| Efficient Frontier Analysis | Especially useful in financial analysis, Efficient Frontiers determine the optimal return that can be expected from a portfolio at a given level of risk |  |  |
| Ranges for adjustable cells and constraints | Streamlined model setup and editing |  |  |
| Genetic algorithms | Find the best global solution while avoiding getting caught in local, “hill-climbing” solutions |  |  |
| Six solving methods, including GAs and OptQuest | Always have the best method for different types of problems |  |  |
| RISKOptimizer Watcher and Convergence Monitoring | Monitor progress toward best solutions in real time |  |  |
| Overlay of Optimized vs Original Distribution | Compare original output to optimized result to visually see improvements |  |  |
| Original, Best, Last model updating | Instantly see the effects of three solutions on your entire model |  |  |






| Feature | Benefit | Professional Edition | Industrial Edition |
|---|---|---|---|
| Optimization under uncertainty | Combines Monte Carlo simulation with sophisticated optimization techniques to find optimal solutions to uncertain problems. Used for budgeting, allocation, scheduling, and more. |  |  |
| Efficient Frontier Analysis | Especially useful in financial analysis, Efficient Frontiers determine the optimal return that can be expected from a portfolio at a given level of risk |  |  |
| Ranges for adjustable cells and constraints | Streamlined model setup and editing |  |  |
| Genetic algorithms | Find the best global solution while avoiding getting caught in local, “hill-climbing” solutions |  |  |
| Six solving methods, including GAs and OptQuest | Always have the best method for different types of problems |  |  |
| RISKOptimizer Watcher and Convergence Monitoring | Monitor progress toward best solutions in real time |  |  |
| Overlay of Optimized vs Original Distribution | Compare original output to optimized result to visually see improvements |  |  |
| Original, Best, Last model updating | Instantly see the effects of three solutions on your entire model |  |  |