Dr. José Raúl Castro Esparza, professor at Benemérita Universidad Autónoma de Puebla, in Puebla, Mexico used @RISK to create a more exact and accurate pricing strategy for a key financial tool, the derivative.
The financial world has an intricate web of tools and methods designed to create wealth. While many of these techniques work well, there still remains a great deal of risk and room for error. Dr. José Raúl Castro Esparza, professor at Benemérita Universidad Autónoma de Puebla, in Puebla, Mexico has used @RISK to create a more exact and accurate pricing strategy for a key financial tool, the derivative. “@RISK allowed us to measure derivative prices by simulating random outcomes in order to obtain a fair price for these financial products,” says Dr. Castro.
Derivatives are, in essence, a security whose price depends on the performance of one or more underlying assets. That is, a derivative’s values is derived from another asset or instrument. Derivatives themselves are contracts between two or more parties governing how the derivative’s value will change based on the underlying asset. Common underlying instruments can include bonds, commodities, currencies, interest rates, market indexes and stock.
Companies often buy derivatives to help manage risk, as these tools can be viewed as a form of insurance policy. For example, an investor may buy currency futures – a type of derivative – to guarantee specific exchange rates before trading in a foreign stock market. Examples of derivatives include futures contracts, forward contracts, options, and stock options. For example, a stock option is a privilege, sold by one party to another, that gives the buyer the right, but not the obligation, to buy or sell a stock at an agreed-upon price within a certain period. As the seller, one wants to charge the buyer a price in the present that approximates the future cost of the underlying asset.
Problems with Traditional Pricing Methods
How does a seller determine this pricing? Traditionally, if a seller was pricing an option to be bought six months in advance, they would apply percent increases or decreases added on for each month (i.e., an extra 15% cost increase or decrease after one month, an additional 15% the next, etc.) This technique, known as the ‘binomial tree’ method, failed to accurately capture real market behavior.
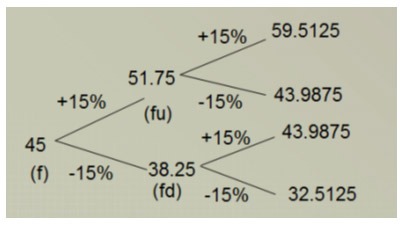
Figure 1: A binomial tree pricing model.
A more accurate technique became available in 1973 when the economists Myron Scholes, Fischer Black, and Robert Merton introduced the Black-Scholes method, which created a more complicated formula to calculate the price (earning them the 1997 Nobel Prize in economics). The technique takes into account the current price of the asset, the average price of the asset during the past, and how many days, months, or years into the future the asset will be bought (i.e. time until expiration of the option). Additionally, the formula incorporates a “white noise” element—which stood in as the inherent uncertainty that could not be measured.
However, “white noise is where @RISK comes into action,” says Dr. Castro. “We modeled that white noise. While the Black-Scholes method assumed derivative values follow a lognormal distribution function, they deviate greatly from that more than 50% of the time.” Indeed, the Black-Scholes method didn’t capture reality. “Real life doesn’t statistically behave in those normal distributions.” In fact, Dr. Castro adds, “Black and Scholes invested their million dollar Nobel Prize money using their technique and ended up going broke. The problem with the Black-Scholes method is that it’s like you’re buying a dress for someone’s girlfriend, but you’ve never met her. Of course you end up buying a dress that is too small or too big. What we did was try to buy a dress that fit right.”
Benemérita Universidad Autónoma de Puebla
From Noise to Knowledge
To find that ‘well-fitting dress,’ Dr. Castro applied a Monte Carlo method, based on the “Random Walk Model” (a mathematical formalization of random movement) that uses the appropriate statistical distribution to model random errors.
Dr. Castro designed an interactive model in Excel VBA so that users could easily access this tool for pricing options. His tool allows users to easily select what company stock they want to buy, what kind of contract they will sign, and the expiration date of the option. Then, @RISK runs thousands of iterations, simulating potential price outcomes for give expiration date. The resulting output is a graph that tells you the different likelihoods of the price for the “call option” (in other words, the compensation that should be paid to the party who is obligated to sell the asset in the future if the option is exercised). For example, the expected value of a call’s premium could be $17.41, and there is a 90th percentile chance it could be as high as $68.32.
@RISK’s customizability and ease-of-use made his option pricing program possible, says Dr. Castro. “I was able to develop this capability with Palisade’s software, creating a much more accurate and simple method of determining the price of these derivatives,” he says.
Dr. Castro’s model has been used as a teaching example in three academic classes: Risk Management, Risk Simulation Modeling, and Financial Derivatives, each with roughly 20 undergraduate and 15 graduate students in the Actuarial Sciences and Master of Finance programs at Benemérita Universidad Autónoma de Puebla.
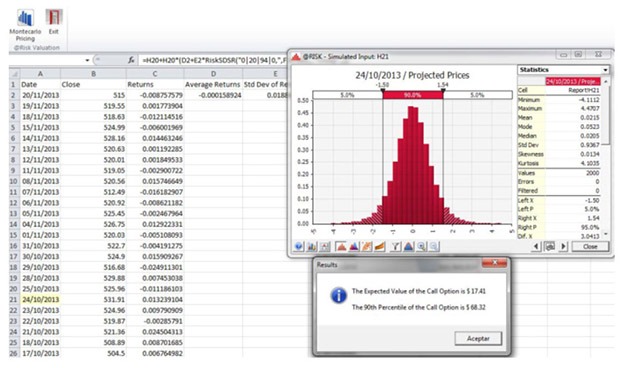
Options prices projected using @RISK
