
To address complicated debt portfolio and capital investment problems, Dr. Emmanuel Donkor uses Lumivero software @RISK and RISKOptimizer. His research has led to new and better methods for addressing financial statistical problems, using @RISK.
When multiple sources of debt with different financing terms are available to the decision maker–for example, a ten-year loan with 5% interest, and a 5-year loan with 10% interest–the environment is fraught with uncertainty. “The challenge is to determine an appropriate or optimal mix of these different debt sources that simultaneously maximizes project value and reduces the risk of default,” explains Dr. Emmanuel Donkor, a quantitative analyst and faculty member of the School of Engineering and Applied Sciences (SEAS) at George Washington University. To address complicated debt portfolio and capital investment problems, Donkor uses Lumivero software, previously Palisade, @RISK and RISKOptimizer. His research has led to new and better methods for addressing financial statistical problems, using @RISK.
Dr. Donkor used Lumivero software tools @RISK and RISKOptimizer to conduct two separate research projects published in the journal the Engineering Economist. The first tackled the improvement of debt portfolios for financing capital investment plans, while the other project empirically tested stochastic dominance relationships in risky capital investments.
Diversifying Debt
In his first project published in the Engineering Economist, Donkor, along with Associate Professor Michael Duffey, addressed the question of how project promoters, who wish to use project finance as a procurement vehicle, can choose an optimal debt portfolio. The aim for these promoters is to develop a portfolio that maximizes project value but minimizes default risk when project cash flows are uncertain, and when debt with different financing terms can be sourced from multiple sources. For example, the promoter may face the previously-mentioned situation of multiple sources of debt with different financing terms—such as a ten-year loan with 5% interest, and a 5-year loan with 10% interest. “It is a difficult problem because the environment is fraught with uncertainty,” says Dr. Donkor.
To address this decision problem, Dr. Donkor and Dr. Duffey used @RISK and RISKOptimizer to help analyze and then recommend an appropriate mix of different debt instruments for financing a capital investment project. “RISKOptimizer allows the analyst to incorporate what’s known as probabilistic or chance constraints—this ensures that the risk of defaulting on loan payments, in any given period of the loan tenure is limited to say 5%,” says Dr. Donkor. They first developed a stochastic financial model in Excel, and used RISKOptimizer’s simulation optimization capability to select an optimal mix of fixed-rate debt instruments such that default occurred no more than 5% of the time. They then used @RISK simulation to evaluate the performance of the debt policy prescribed by the optimization model.
This new approach improves on the traditional methods used in risk analysis in capital investment planning, in which analysts would “take the value of debt as given, and simulate it without taking into consideration the probability of default on debt service each year,” says Dr. Donkor. “Furthermore, analysts do not consider multiple sources of debt with different financing terms—you hardly ever see debt portfolios with different terms and interest rates—it’s usually homogenous, with debt having one tenure and one interest rate.” Dr. Donkor and Dr. Duffey’s new approach, which shows how to model chance constraints in a spreadsheet environment, and implement it with RISKOptimizer, has sparked interest in the field. The paper detailing their work has become one of the highest ranked articles in the Engineering Economist.
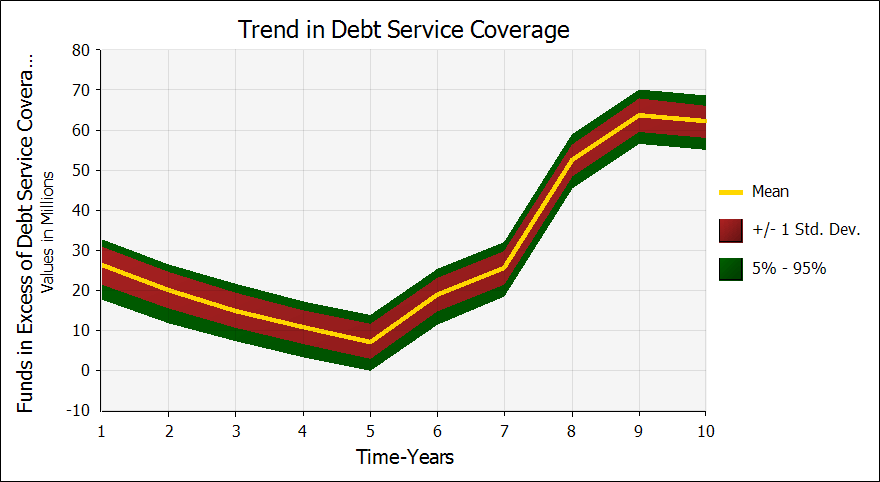
Figure 1: The profile of excess earnings after debt service, indicating that the chances of defaulting on debt service are well contained.
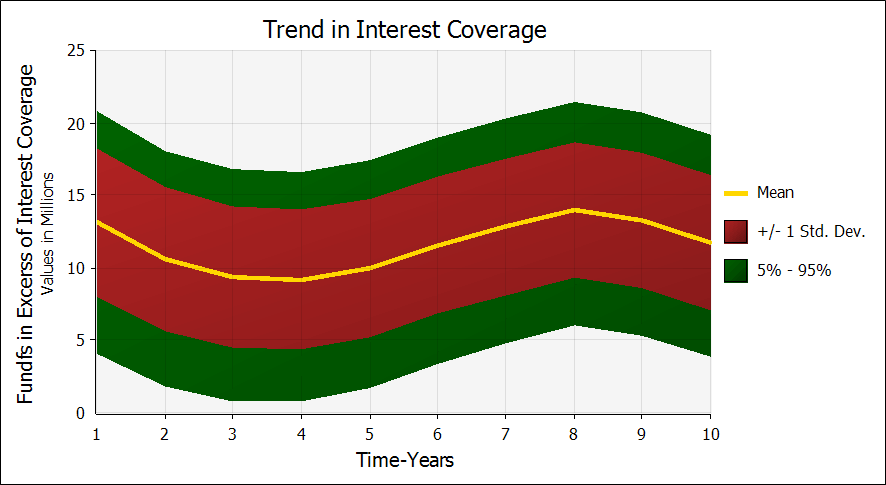
Figure 2: Plot of excess earnings after interest coverage.
School of Engineering and Applied Sciences (SEAS), George Washington University
Ranking Opportunities
Dr. Donkor also addressed the problem that analysts face when they must choose between multiple, risky, mutually exclusive capital investments. He did this by creating a spreadsheet framework that uses @RISK to implement empirical tests of stochastic dominance—a term used in decision theory which describes the ranking of random prospects based on preferences regarding outcomes. As a result of Dr. Donkor’s work, analysts involved in comparing risky capital investments do not have to rely on qualitative and visually-based ‘best guesses’.
This solution benefits those who are faced with investment choices in which only one option can be selected. For example, a person owns a building, and has to decide whether to rent it out as residential apartments or as a factory. “You can’t do both at the same time,” says Dr. Donkor, “so you have to choose one option.”
Typically these kinds of opportunities are compared by using decision rules based on the mean-variance criterion (selecting portfolios based on the means and variances of their returns) or safety-first criterion (setting a minimum required return for a given level of risk). However, at times, the mean variance criterion and its variants result in an efficiency frontier in which more than one investment option offers maximal expected return for some given level of risk, and minimal risk for some given level of expected return. This can make it difficult to select only one option.
“The problem becomes complicated when you have opportunity A, which gives you the highest value, but it has a high risk, and opportunity B, which will give you lower value but a lower risk,” says Donkor. “As a decision maker, you want high value and low risk, but these qualities are not always enshrined in the same opportunity.” For such problems, stochastic dominance rules, typically implemented by visually inspecting the cumulative distribution functions (CDF) of the alternatives, are applied. However, for many practical applications, it is common for the distributions to cross tails, creating what’s known as the ‘tail problem’. In these circumstances, analysts apply what’s known as ‘almost stochastic dominance’ (ASD), which allows decision makers to ignore the crossing at the tails so that dominance inferences can be made.
These approaches are inexact and lack quantitative certainty; on top of these issues, Dr. Donkor says that most analysts do capital planning problems in Microsoft Excel, but are not able to make stochastic dominance inferences in that program. “A theory has been developed, but no one has turned that theory into a code in Excel where it can be used,” says Dr. Donkor. Thus, the majority of practitioners, researchers, and students who analyze alternative capital investment plans under uncertainty in Excel are limited to using either visual inspection or ASD without any empirical support.
Dr. Donkor has improved this process with his @RISK-enabled spreadsheet framework which empirically tests stochastic dominance. Now, instead of using a visual best guess, analysts can use an @RISK model to empirically test for the best option among many, allowing them to make empirically defensible decisions when comparing risky capital investments.
Originally published: June 16, 2021
Updated: June 7, 2024
