
'@RISK has been an important tool in the creation of African Risk Capacity Insurance Company Limited (ARC Ltd), Africa’s first sovereign catastrophe insurance risk pool. ARC Ltd has been using @RISK software since it was first set up in 2013 to support complex modelling of drought losses across Africa for insurance and reinsurance pricing purposes as well as dynamic financial analysis to model ARC Ltd’s long-term financial sustainability.
Case I: Using @RISK to Simulate Drought Losses Across Multiple African Countries
ARC Ltd provides insurance against drought risk to African governments. The insurance pays out based on satellite rainfall data that feeds into a drought index which is then converted into an estimated cost of responding to the drought. This is done through ARC Ltd’s software Africa RiskView.
ARC Ltd can therefore calculate what the drought response costs would have been for each African country for the past 30+ years of historic rainfall data. Based on this historic data, ARC Ltd uses @RISK to simulate the drought losses over longer time periods. And based on these simulations, an accurate price for transferring the drought risk to ARC Ltd can be calculated.
ARC Ltd insures multiple African countries on an annual basis and buys reinsurance to cover the overall portfolio. It therefore needs to calculate the price of reinsuring itself every year.
Reinsurance focuses on transferring tail risk, which is the risk of very rare but severe events occurring. To model ARC Ltd’s insurance payouts for reinsurance purposes, a minimum threshold is set for each country’s losses -only very severe losses above this level are therefore included.
Assigning a cumulative non-exceedance probability to each country’s historic as-if severe losses, ARC Ltd inputs these points using @RISK’s Distribution Fitting tool, opting for a cumulative distribution function.
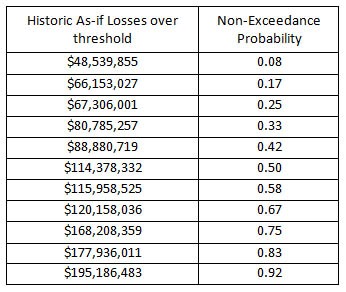
Table 1: A given country’s historic as-if drought response costs over $45mn threshold during the past 30 years and corresponding non-exceedance probability value.
@RISK gives the option to suppress questionable fits which cuts down the number of potential curves from which to choose.
The fitting tool ranks the various curves by a user-selected measure of error and plots the input data as well as the curves selected. The visual aid helps to rapidly assess which of the curves are most appropriate as one can see which curve best represents the tail risk. The latter is very important for accurately modelling extreme risks within a reinsurance context as an overestimation of tail risk results in higher costs for the reinsurance cover while an underestimation of the risk leaves the insured unknowingly exposed to major disasters.
Additionally, @RISK provides a chart of statistical data giving the input data’s mean, median, standard deviation and other key figures in comparison to each curve’s data as shown in Figure 1. This helps to quickly assess which curve best matches the underlying data’s average expected loss, another important criterion in the curve-fitting process.
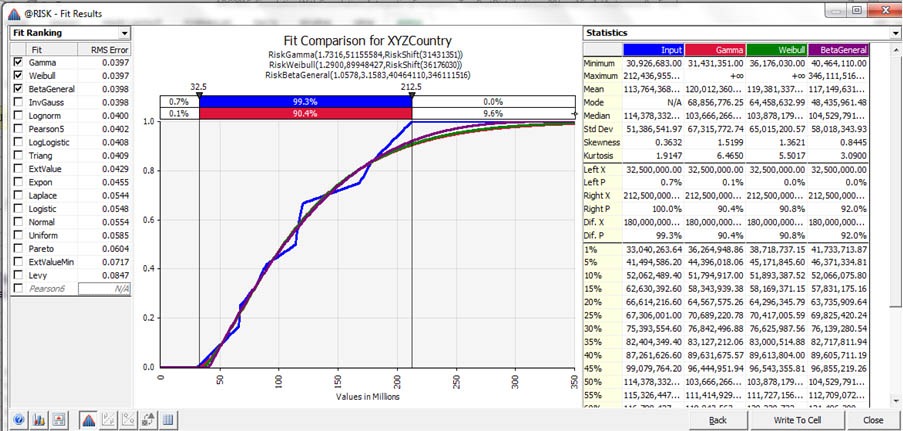
Table 1: A given country’s historic as-if drought response costs over $45mn threshold during the past 30 years and corresponding non-exceedance probability value.
Once an appropriate curve is chosen for each country, the formulas can be correlated in @RISK. This is important in ascertaining the overall level of risk at the portfolio level. For example, if two countries have risk that is highly correlated, the portfolio’s overall risk will be higher.
Using Excel’s correlation function CORREL, ARC Ltd creates a correlation matrix based on the historic as-if loss dataset. This matrix is then used to link the formulas through @RISK’s Define Correlations tool. The correlation appears as another parameter in each curve formula.
Lining up the distribution formulas in a row, @RISK can now generate simulated losses for each formula using the RiskData function. The simulations can be run at varying iterations which gives ARC the flexibility to run quicker 1,000-iteration simulations to check the output and do test runs before running the major 20,000+ iteration simulation.
The simulation output (the simulated country losses) are then run through the countries’ risk transfer parameters to give ARC Ltd’s total loss for each iteration. This gives an overall probability distribution for the portfolio (for extreme risks) which is used to estimate what portion of risk should be retained and what should be transferred through reinsurance and at what price.
Case II: Using @RISK For Dynamic Financial Analysis Of Arc Ltd Appropriate Capital Base
ARC Ltd also uses @RISK extensively in its DFA modelling. This utilises Monte Carlo simulation techniques to sample a wide variety of possible outcomes for a financial (insurance) entity and provides a probabilistic summary of financial results for a forward-looking window.
The Monte Carlo technique comprises the running of a large number of simulations -at least tens of thousands- with each simulation sampling from probability distribution functions for one or more inputs, most importantly annual insurance payouts.
ARC Ltd uses DFA to test various portfolios of risk (i.e. different countries and coverages), priced at different rates, with different initial capital and different reinsurance strategies. Other items such as investment return, operational costs and reinsurance pricing can also be varied.
Using @RISK, ARC Ltd carried out initial DFA modelling before the entity was set up to test and stress these multiple inputs and their impact on the capital base over a 20-year period. Another round of DFA modelling was carried out in 2015.
In the latest round, ARC Ltd calculated an exceedance probability distribution (EP curve) for the portfolio for each year over an 18-year period, taking into account the growth in the portfolio over that window period and the change in risk profile.
Using @RISK, a 10,000 iteration simulation was run that sampled random loss points from each year’s portfolio EP curve and fed these through a given case (i.e. with insurance price/premium, reinsurance price, investment return, operational costs and capital injections set at a certain level). This gave a range of 10,000 outputs for the value of shareholder equity over different time-frames. This was translated into a “probability of survivability” over these windows. Figure 2 shows shareholder equity values at the end of 2020.
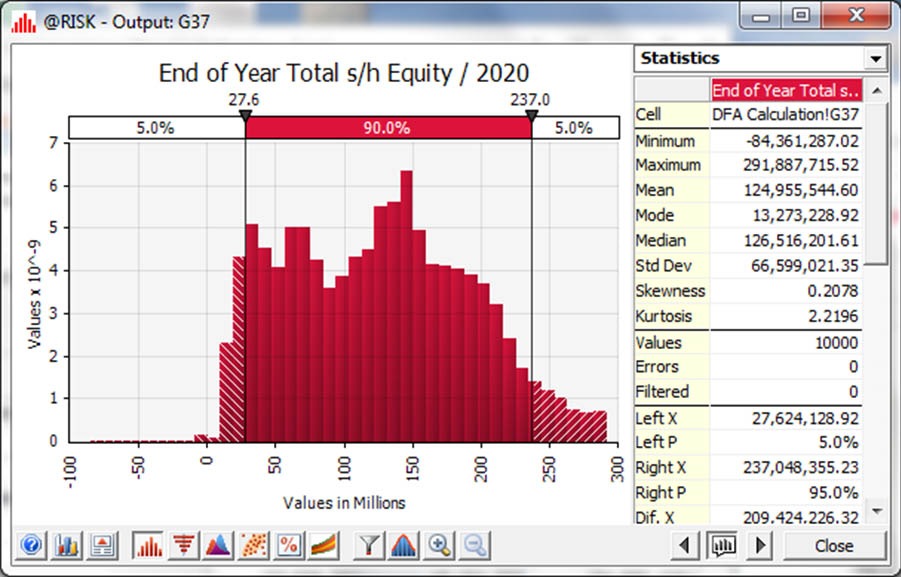
Figure 2: @RISK visual output of 10,000 simulation in DFA modelling process to ascertain probability distribution of ARC Ltd’s financial results over a five-year period.
This process was repeated across multiple cases which stressed each input parameter or used different portfolio EP curves that assumed faster or slower portfolio growth rates.
@RISK made it straightforward to summarise each case's output by clicking on Excel Reports in the @RISK menu and opting for simulation data.
