
Continuing with this series of articles introducing cost estimating with @RISK, we will compare the use of the most popular distributions of this technique: the Triangular and the PERT.
We know that cost estimation is one of the most critical parts of project management. In addition, we know that three-point estimation – with PERT or triangular distributions – is widely used in this endeavor, but we need to point out that these distributions have different characteristics. The purpose of the following lines is to present them and provide an informed opinion of their use in estimating.
How do three-point estimates work?
Three-point estimating is a simple but useful approach to estimating the cost of the elements of a budget.
There are three different values that are typically obtained from suppliers (from their quotes) and/or from an expert's judgment:
• Optimistic estimate or best-case scenario (lowest cost in this case).
• Pessimistic estimate or worst-case scenario (higher cost in this case).
• Most likely estimate or most realistic scenario
For example, we can have a development task that if everything goes fairly well and we do not have any serious impediment, then the task will last 5 weeks.
However, if we have problems with the code, we could see the construction of the software stretch to up to 10 weeks. On the other hand, if we manage to elaborate this part quickly, we can overlap tasks and conclude the project in 4 weeks.
Therefore the 3 points of the estimation would be:
P = 10 weeks
Ml = 5 weeks
O = 4 weeks
A three-point estimate can be represented by a distribution like the triangular and PERT which belong to this family of continuous probability distributions defined by the minimum (a), most probable (b) and maximum (c) values that a variable can take.
Let's see below a Triangular distribution and a PERT distribution:
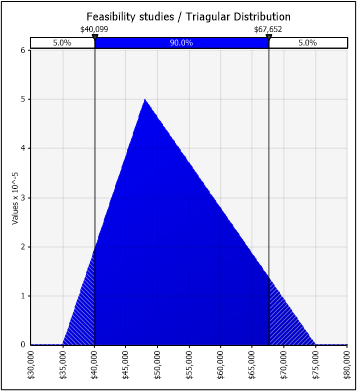
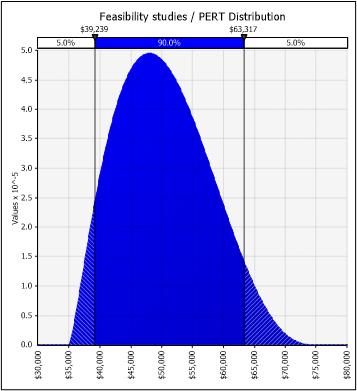
The PERT method allows us to convert the three-point estimate into a smoother curve by assimilating a Normal. When the distribution is skewed, the PERT distribution provides a more "natural" shape than the corresponding Triangular distribution.
The Triangular main drawback is its unnatural shape, which rarely, if ever, describes a natural process adequately. In comparison to the PERT distribution, it tends to overestimate the tails and underestimate the shoulders.
Let's see a comparison between the Triangular and a PERT distribution:
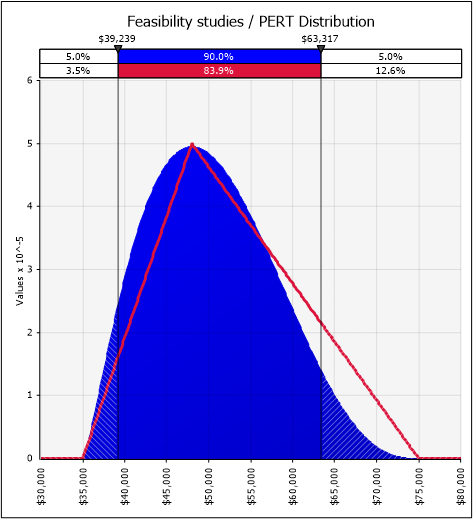
Considering the above, using the triangular method is recommended when there is no history of similar projects, as there is no basis for giving a particular estimate more weight. Therefore, the triangular distribution is more suitable for expert judgment estimates or rather guess estimates.
Note: Comparative analysis of two or more distributions can be done using the overlays’ function offered by @RISK in the distributions panel.
An example in @RISK
Continuing with the example of the previous article, we will explore the use of distributions in a cost and contingency model.
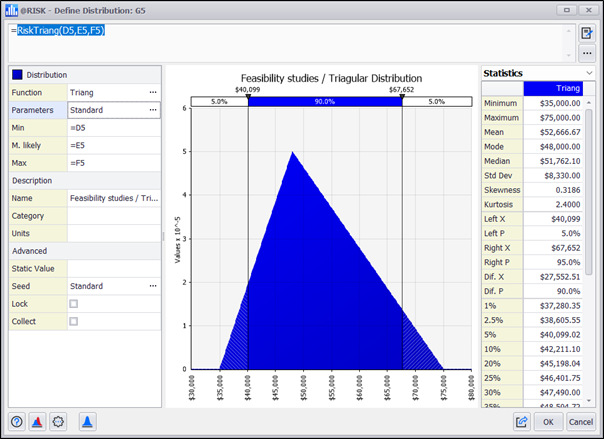
In this case we are going to add two columns with the estimates represented with the Triangular and the PERT:

We can now configure each cost element using the @RISK functions to design the distributions:
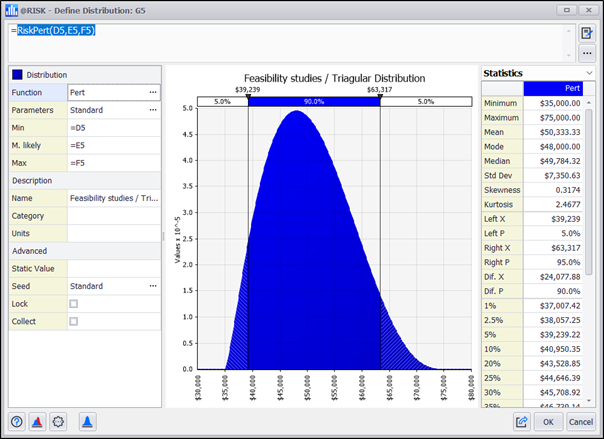
The next step is to complete all cost elements with the corresponding formulas:

We sum each of the columns to have all the deterministic and probabilistic scenarios in order. We then declare the totals of the probabilistic columns as outputs of the Monte Carlo simulation model:

![]()
We are now ready to run the simulation. Let's test with 1000 iterations and see the effects on the results:
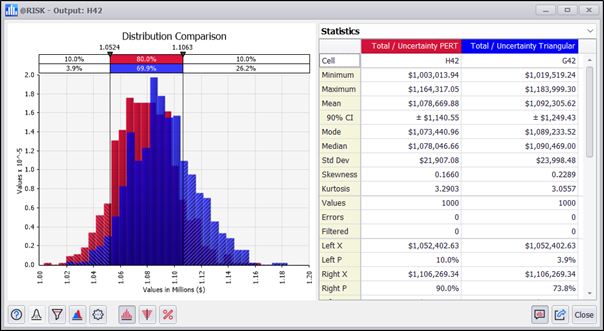
This process will take a few seconds in @RISK and will generate 1000 independent combinations of our cost items and their corresponding results:
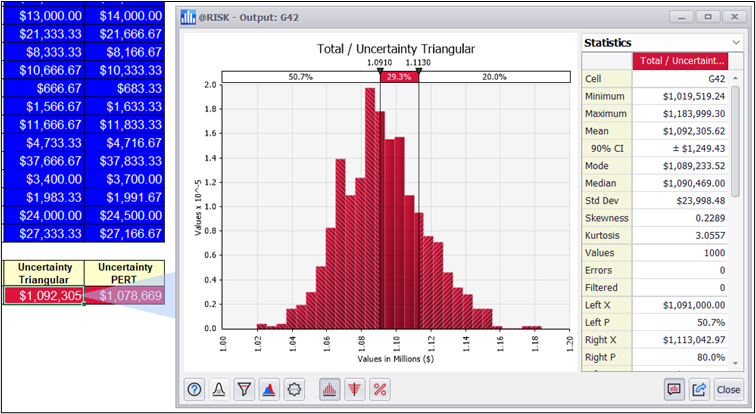
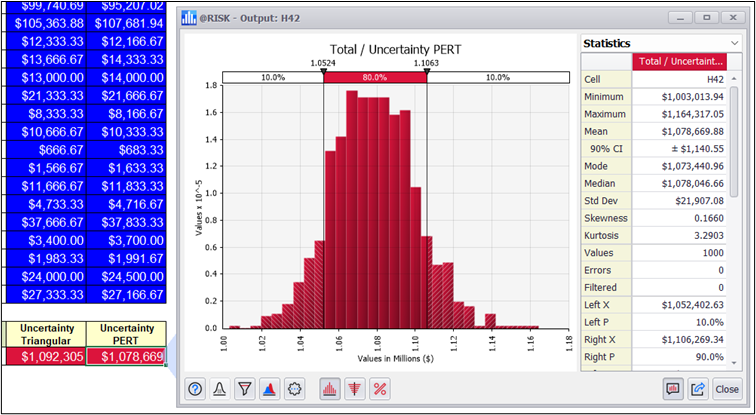
The distributions of results are similar, but if we look at their descriptive statistics, there are some differences to consider:
Conclusion
Three-point analysis can benefit from the PERT distribution as an alternative to the triangular distribution. One advantage of the PERT is that it has a smoother shape than a triangular distribution, with an emphasis on the most probable value. Although we are interested in the mathematics of the triangular distribution when we are unsure of the weights given to the expert criteria.
The correct selection and combination of the distributions, facilitated by the simple use of @RISK, allows us a more justifiable and solid analysis for our decision-making when cost estimating.
Try this for yourself by downloading your 15-day free trial of @RISK.

