Decision Analytics






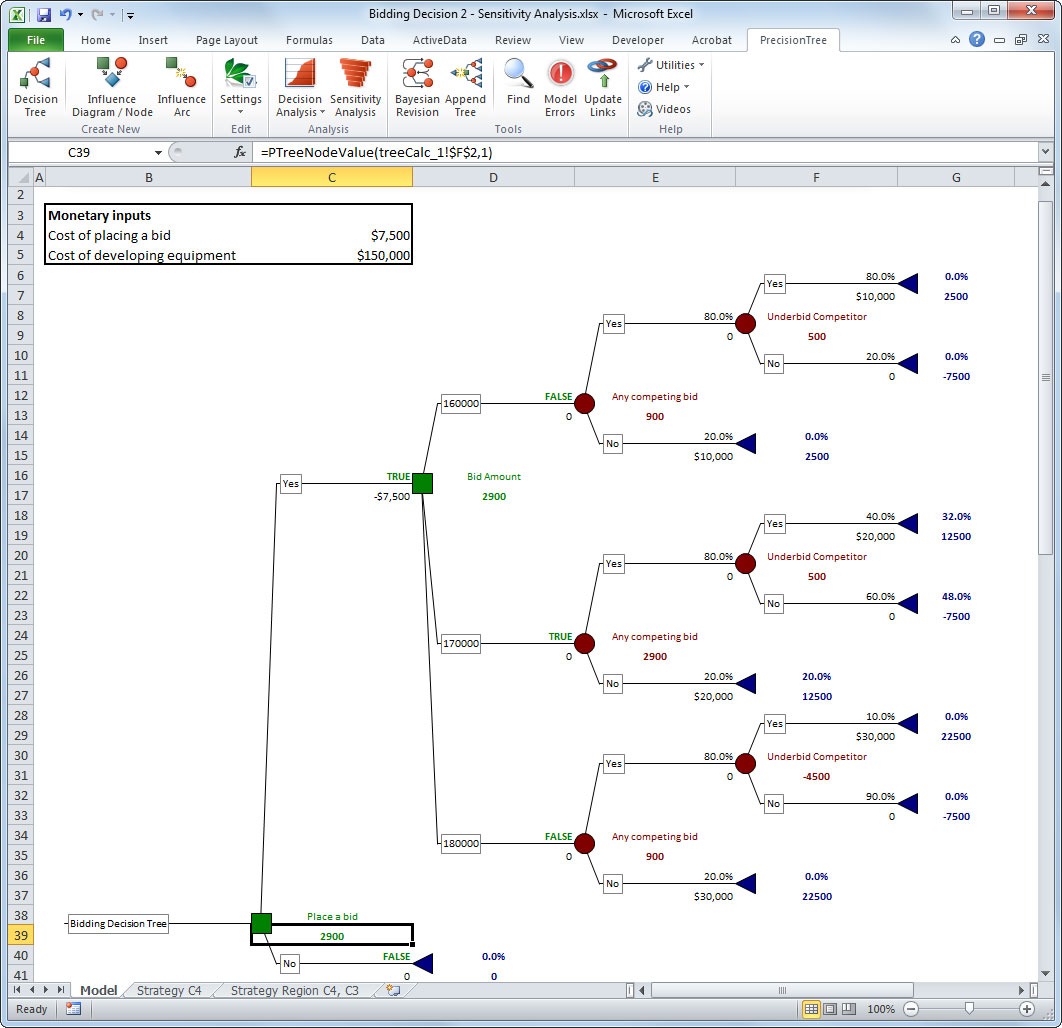
Decision trees are among the most popular decision analysis techniques, owing to their visual and interactive nature. Decision trees allow you to map out decision options and chance events (typically from left to right) using nodes and branches. They support probabilistic calculation of uncertainties, adding a quantitative, defensible aspect to the analysis that complements the communication benefits of seeing different decision paths. This makes them ideal for multi-stage, sequential decisions of all kinds. Decision trees are flexible enough to provide insights into both simple and complex decisions, often supporting reference and logic nodes to enable larger models. Utility functions can be incorporated into the analysis, giving a new lens through which to assess the worth of objectives. They can also include sensitivity analysis, allowing decision-makers to understand which factors in the model lead to different outcomes.
Decision trees are available for any analyst at the desktop level, directly within Microsoft Excel. This provides maximum modeling flexibility with a minimal learning curve.
Like decision trees, influence diagrams are visual and mathematical representations of decision situations. They were first developed with the goal of creating a model that was intuitive and easy to understand, thus aiding in team decision analysis.
Influence diagrams consist of nodes representing uncertainty (probabilities), decisions, and values (payoffs). The nodes are connected by arcs, which are functional (ending in a value node), conditional (ending in an uncertainty node), or informational (ending in a decision node). Unlike decision trees, influence diagrams are not sequentially structured. Influence diagrams are meant to show (see below):
Like decision trees, influence diagrams are available for any analyst at the desktop level, directly within Microsoft Excel.
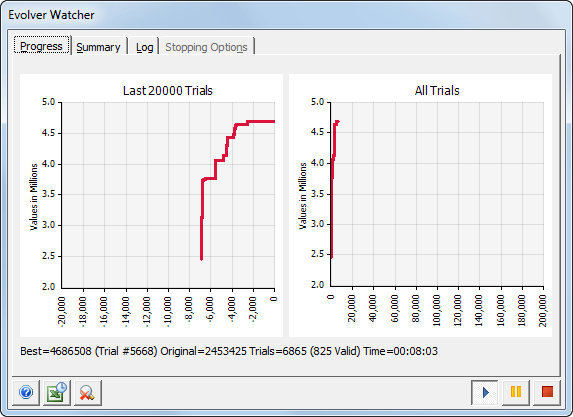
Optimization is the use of mathematical models to analyze many different solutions to a problem in an effort to find the best one suited to your stated objective. That objective could be maximizing something like profits, minimizing something like costs or variability, or achieving a targeted value of some kind. Typically, there are many decision variables and constraints on resources like time and money. The result is an allocation problem, where the best distribution of resources, or the best order in which to do things, is not obvious. Examples of such problems include how to schedule a fleet of trucks, the best pricing strategy for airlines and hotels, portfolio allocation, production scheduling of machines and workers, inventory management, and supply chain strategy. Optimization software tries many different combinations of possible allocations, subject to resource limitations, to best achieve your stated goal (see below). The result is a prescriptive “answer” to guide the user on the best strategy.
Though computationally intensive, optimization tools are available at the desktop level for any Excel user, where many decision-makers share and construct decision models.
Some practitioners view decision analysis as a form of risk analysis, while others view it vice versa. Either way, there is no doubt the two disciplines are connected, and both improve overall decision-making.
One way that risk analysis can be used to enhance decision analysis is through the application of stochastic risk analysis, or Monte Carlo simulation, to decision analysis. In most cases, decision analyses only concern themselves with multiple discrete outcomes. Typical decision analysis methods are unable to account for the real-life continuous nature of what are effectively infinite outcomes. This is an area to which Monte Carlo is well-suited.
