Cynametrix, a financial analytics consulting firm based in Minnesota, uses the DecisionTools Suite to help them integrate life insurance products into general financial analysis. Traditionally it has been difficult to evaluate life insurance within a broad financial portfolio, however Palisade’s DecisionTools Suite solves this problem via Monte Carlo simulation and optimization to incorporate life insurance products along with all the other financial variables present in investment analysis. Thus, Cynametrix is able to demonstrate precisely what the financial advantages are of one decision over another to clients.
Background
Traditional financial analysis has focused heavily on various aspects of asset allocation decision and portfolio optimization. According to modern portfolio theory, adding an asset which has returns that are not tightly correlated to other assets in that portfolio can mitigate the risk of overall loss for that portfolio by reducing volatility. Thus, portfolio designers can optimize portfolios to yield either the highest expected return of a portfolio for a client’s given level of risk aversion, or the lowest level of risk for a client’s desired expected return.
Life insurance, or Insured Death Benefit (IDB) is a useful class for optimizing portfolios because its rate of return is driven primarily by when death occurs, rather than fluctuations in the capital markets, which means that IDB returns have a low correlation to those of other asset classes that are dependent on the stock market’s performance.
This idea is important not just for individuals and the assets they leave their families, but also for multi-life situations such as high-net worth families who pool their financial management, large charities such as colleges that have an insurable interest in their major donors, and businesses who must fund executive benefits such as deferred compensation plans.
Until recently, most analysts and scholars overlooked IDB as a usable product for a traditional investment portfolio. This was because IDB is difficult to compare to other traditional assets like securities or stocks, as IDB can manifest in two separate ways—either as cash value— the investment element of a policy that is paid to the owner if the policy is surrendered prior to death, or as the death benefit, which is the amount paid to the policy's beneficiary at the insured's death. “The problem is, when you evaluate an IDB it’s hard to compare it to securities,” says Robert Danielsen, CEO of Cynametrix. “What are you going to evaluate? The cash build-up or death benefit? Historically, insurance people have talked about the two characteristics separately.”
Optimizing portfolios with life insurance also presents a problem. Danielsen explains that, for portfolios with traditional financial products, analysts use the annual expected mean return and variance of an asset class to optimize the return or minimize portfolio instability. However, with life insurance products “there’s only one point of return—that’s the death of the insured, and we don’t know when that is—so how do you integrate that?”
A New Approach to Life Insurance
Danielsen tackled these problems with IDB by creating a proprietary mathematical process known as MAVsm(which stands for mortality adjusted value) The process generates values and indexes for valuing the cash position of any life insurance product or strategy, incorporating mortality probability. Essentially, Danielsen conceived of the idea that, at any point in time the future cash position of an IDB can only be one of three things:
- Cash Value, if the insured has not died
- Death Benefit, if the insured dies at that point, OR
- Reinvested Death Benefit, if the insured has already died
Thus, Danielson derives the following formula:
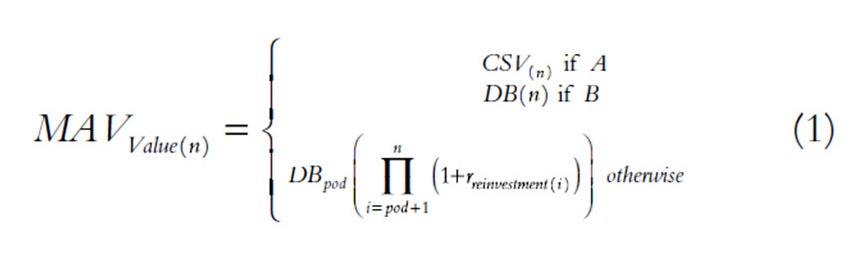
Where:
Using his proprietary MAVsm technique, Danielsen uses Monte Carlo simulation to determine which of these three options the IDB will be for any given year in the future. “The process necessarily requires Monte Carlo simulation—I don’t believe what we do with MAVsm can be done with a static formula—it’s all probability-based,” says Danielsen. “It’s a perfect example of what the Palisade products can do.”
Because there is no way to know for certain when the insured person will die, Danielsen incorporates mortality probability data into @RISK, and runs the model several thousand times. The MAVsm method also incorporates myriad other variables, including product issues, investment decision, and tax attributes—all of which requires a workbook with 12 worksheets with over 250,000 active cells to take all these variables into account. “There’s no way the human brain can see the relationships among all these variables, all of which are probabilistic,” says Danielsen. “That’s why Monte Carlo simulation is so necessary for this work.”
For example, Figure 1 is a histogram of the results of a Monte Carlo simulation of the age at death for a 54-year old male non-smoker, using standard actuarial tables with certain adjustments. Because the age of death determines the MAVsm value at any point in the future, the probability of death at each age, as demonstrated in this simulation, can be combined with the other variables of the model to determine the statistical properties of the MAVsm value at any point in the future. These simulation results show that by year 20, for example, the probability is approximately 12 percent that the insured has died and that the death benefit has been received. It also shows that there is a 1% chance of the person died that year. Finally, the likelihood that he has not died yet, (and that life insurance still exists as its cash value), is 88%.
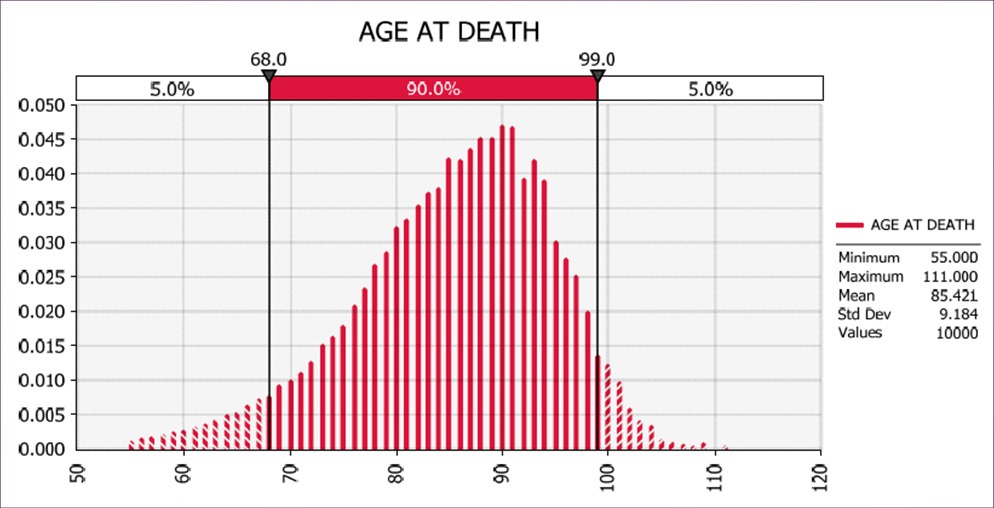
Figure 1: Mortality Probability by Age at Death (Male, age 54, nonsmoker): Graph shows probability of death in Year 20 is only ~1%, and the probability of death by Year 20 is ~12%
Along with this IDB data, the final result of Danielsen’s MAVsm model also includes a distribution of thousands of possibilities for the securities portfolio for each year of the strategy. Using this projection of probable values allows Danielsen to see the overall risk-adjusted returns of the portfolio.
With this information in-hand, Danielsen can then test the effect of different allocations of the portfolio to IDB to determine whether IDB is improving the probable risk-adjusted returns of the entire portfolio. Using RISKOptimizer, he also determines the optimal allocation of the portfolio to IDB, as well as the optimal allocation among a number of potential insureds in a multi-life case.
This approach to incorporating life insurance into financial portfolios is unprecedented, says Danielsen. “No one else is doing this, to the best of my knowledge,” he says. “When we show it to clients, they say they’ve never seen anything like this.” The alternative approach only compares a selected number of scenarios, based on static variable assumptions. “There is no way to evaluate the relative probability of the selected scenarios, much less combine the probabilities of the many variables in order to see the interdependent effects among the variables,” says Danielsen. “This made much of the planning a shot in the dark.”
Thanks to Palisade software, Danielsen has been able to make planning as precise as possible. “Palisade products have really enhanced these optimizing methods for me, and helped me create a much more sophisticated product.”